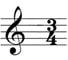Throughout my career as a teacher of music, it has often been assumed by colleagues that my mathematical ability would be similar to my musical abilities. Fortunately for me, my mathematics is not too shabby but is this evidence enough to make a firm link between these two different disciplines? The connection between mathematics and music is not a new one and in this article, I am going to explore this fascinating idea a little further.
Classical Music and Mathematics
The notable Greek Mathematician and Philosopher Pythagoras made some of the earliest recorded connections between mathematics and music. It was Pythagoras who discovered the relationship between the changes in the tone of vibrating strings and how they are divided. For example, if the length of two strings is in the ration of 2:3 the difference in the produced pitch or tone is that of a fifth (eg: D – A). His work, in turn, was then further discussed and developed by Plato in his work “The Composition of the Soul”.
In a less complex fashion, we can also find a connection between the two subjects in terms of rhythmic division. If we consider traditional musical notation, the first thing we observe next to the clef is the ‘time-signature’ (see fig.1)
Figure 1.
These two figures tell the performer how each bar of a piece of music is divided. In the case of 3/4, then each bar has three crotchet beats in it as a maximum value. The bar could include a whole variety of different musical values that add up to three crotchets (one-beat notes), and here again, the mathematics comes into play.
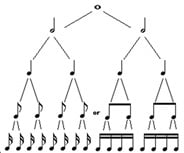
This leads on to the division of note values which in themselves can be viewed as mathematical in their relationship to one another. (See fig. 2)
Figure 2.
This figure illustrates the division of the semi-breve (top) into increasingly smaller note values; effectively dividing by two each time.
Metronome markings can also be thought of a link to mathematics. This musical indicator tells the performer the precise speed of a piece of music as opposed to a verbal representation of the speed. By this I mean, often composers write Allegro, Andante, Adagio, to give an indication of the speed and nature of their composition but these words do not convey an exact speed or tempo of the piece. A metronome marking is a numerical representation of the tempo of the music. If the composer wishes the piece to be played at one crotchet beat per second then they would write a metronome marking of crotchet equals 60. (See fig.3)
Figure 3.
Likewise, crotchet equals 120 is exactly twice the speed of the above marking; or crotchet equals 180, three times a fast.
Arnold Schoenberg invented a completely revolutionary method of musical composition that became known as Serialism. Schoenberg created this compositional tool to break away from the traditional tonal system of writing music. In Schoenberg’s approach, he allows each note of the chromatic scale to be of equal importance and abandons the concept of tonality altogether. His students, Alban Berg and Anton von Webern adopted this method of composition, both in very different ways, but both based on what came to be known as ‘tone-rows’.
These tone rows formed the basis for the compositions, providing musical material on which to base the work. The construction of a tone-row, according to Schoenberg’s principles, meant that no note could be used again until every other note of the chromatic scale had been included. This effectively meant that all twelve notes of the chromatic scale were employed in the tone-row equally.
From these ideas, you can begin to understand how mathematical the process of composition can become. Later composers such as Boulez, Carter, Stockhausen and to an extent Messiaen, produced compositions in which almost every aspect of the music was determined by ‘serial’ processes from the pitches though to the rhythmic divisions and the entire structure of the work. The effect on the composition needs to be heard to be appreciated. For many people, this move towards a more mathematical process for music was simply a step too far and in some senses almost removed the possibility for everybody to be able to access the results.
In the work of the Greek composer Xenakis, he applied the principles of stochastic mathematics directly into his musical composition. His claim was that this method could be used by anyone with a basic grasp of mathematical concepts, but my feeling is that he somewhat overestimated the complexities of the task. Xenakis produced some remarkable compositions, were for me, the musical outcome is not overshadowed by the underlying processes. One of his ground-breaking works was the 1954 composition titled “Metastasises”, in which Xenakis uses 12-tone methods and the Fibonacci series to explore Einstein’s view of time. The music directly links to mathematics in an open and honest way that, to my knowledge, no other composer had achieved before. The results are breath-taking and uniquely beautiful.
Music of the 20th and 21st Century is not the first Classical music to incorporate mathematical concepts into its design. Among many composers, Bach is often cited as exploiting mathematics in his works in creative and distinctive ways. As far as we are able to know, Bach was reportedly fond of the number 14 and it’s reverse, 41. Why 14, well if you assign each letter with its number with A as the first letter you get the following: B = 2; A = 1; C = 3 and H = 8, giving a total of 14. In Bach’s “Goldberg Variations” this number runs like a structural thread through the 14 canons. In “The Musical Offering”, there is a number of articles professing the mathematical link to the contrapuntal music Bach composed. This extends to being able to express each of the canons as a mathematical function.
The deeper you look for connections between mathematics and music the more you will find. Perhaps the important thing to keep in mind is that mathematics is not simply a way of solving problems or proving concepts and musical composition is not only a method of organising sounds. The beauty of both disciplines is how seamlessly they can work in tandem to enable us to explore and express our ideas.
Read: